Möbius and Riemann Zeta functions – their most natural explanation

Möbius function, although being one of the fundamental ones in number theory seems to be purely theoretical one, with no reflection in “reality”.

But there exists its very clear and also the most natural representation – Möbius function describes the positions of the relatively prime unities on the NumbersPlane.

A detailed explanation of the idea of the Numbers Plane (the most natural representation of the numbers) can be found here, and in the video linked there.

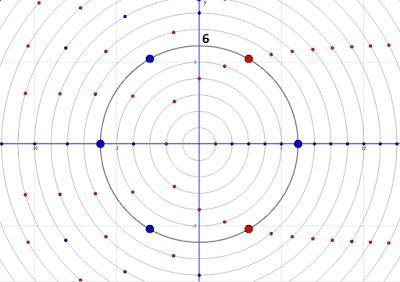
Let’s take as an example the number 6 and its representation (including its pattern of divisibility – red unities are relatively prime, and the blue ones are the not relatively prime)  on the Numbers Plane.

When we sum up the coordinates of all the unities representing given number on the Numbers Plane they naturally always (for every number n) sum up to 0 (both X and Y coordinate).

But when we sum up coordinates of only the relatively prime unities, then we are always getting the value (it’s the value of X coordinate, because Y always balances to 0, since the Plane is symmetric about the X-axis) equal to n*µ(n)

So for n=6 we are getting the value 6 (6*1), for 5 the value -5 (5*-1), and so on.

So simplifying, actually, the Möbius function shows generally the balance of the relatively prime unities within the given number n – whether they are generally shifted more to the left (then the value is “-“), or right (then the value is “+”) side of the origin or they are perfectly balanced for n not being the square free.

And looking at the patterns of divisibility of the numbers on the Numbers Plane, it’s easily understandable why the Möbius function behaves in such a way (why it takes exactly the certain values for given n).

Looking at the position of the relatively prime unities of the numbers we can get also the direct value of the Möbius function (not being multiplied by n)

Let’s apply to every unity a unit vector directed in opposite direction (or towards - it changes only the sign of the result) to the origin. 

Then all the unity vectors applied to the relatively prime unities or not relatively prime ones (red or blue) will always sum up to the value of the Möbius function for the given n.

Whether it’s the value or negative value of the Möbius function depends on the direction of the unit vectors we are considering (toward the origin, or opposite).

Generally, the idea of application of some kind of values/magnitudes to the given kind of unities (relatively and not- primes) – these might be forces, charges, spins etc. – could be very useful (I would even say that might be fundamental) for the analyses of all kinds of physical interactions and fields.

Different types of hypothetical interactions may depend in different ways on the distance. 

So we can ignore the influence of the distance (in our case - for simplicity - individual unity from the centre of the system), or use directly distance n, or n^2, or any other power of n.

Doing so, we are moving to the “real” meaning of the Zeta function – which is just the inverse of the value of the resultant of the forces/interactions applied to the unities representing the relatively primes (or those not) measured in the origin.

It’s in full accordance with the very well-known formula tiding both functions.

So looking at the left side of the equation:

• for s=0 (so omitting an additional influence of the distance from the origin) we’ve got just pure value of the Mertens function, which in fact represents the resultant of the unity vectors applied to all the relatively primes up to given n. So we can say that it shows a kind of balance of the relatively prime unities on the Numbers Plane - how much do they all together somehow lean towards the left or right side of the coordinate system.
• any other value of s shows just the force of the interaction applied to the relatively prime unities influencing only the magnitude of the final resultant
• and specifically for s=-1 we are getting the value of the resultant of the coordinates (the X one, while Y always balances to 0)

And this is a very good starting point for considerations on the Riemann hypothesis…

The infinite symmetry (symmetry of patterns of divisibility in any possible direction) of the Numbers Plane shows the beautiful, full order of the arrangement of the numbers (and of course at the same time primes) and I personally believe that in fact implies the Riemann hypothesis (at least, the proof can be directly derived from it).