On the density of Euler’s Phi function of the sets of numbers in form of p+/-n and their relation to Artin’s constant
It’s well known that the average density of Euler’s Phi (totient) function (stated as Phi(n)/n) within all the natural numbers, or their long enough subset (including randomly chosen) is equal to
We can wonder then what are the average densities of Phi of some specific subsets of the Natural numbers.
Creating such a subset starting from some number m and including into it every nth number (so for example starting from 5 and taking every 3rd one: 5, 8, 11, 14…) makes the case trivial – as expected such average density (let’s call it D(S)) is simply dependent on the divisors of m and n (arranged in a simple formula and multiplied by the 1/Zeta(2) ), so it’s not worthy of being considered here.
That’s why the average density of Phi of even numbers is equal to
and odds is equal to
It's also obvious that the density of the set consisting of only primes naturally tends to 1 when the size of the set tends to infinity, since the Phi(p) = p -1
But the case becomes less trivial when we consider the sets in form of p+n, where p denotes the set of all primes, and n is any fixed natural number.
One could expect that the density of such the set would tend to the average density of evens or odds once the n being added to the primes is odd or even since we are adding fixed number n to the “random” set of all the primes.
But this is not what happens.
Let’s take the first such set, where n=1. It would consist of following numbers: 2+1, 3+1, 5+1, 7+1, 11+1, 13+1,…
So, S[p+1] = 3, 4, 6, 8, 12, 14, 18, 20, 24, 30….
Unexpectedly the average density of Phi of the numbers within this Set is equal to the well-known Artin’s constant.
Artin’s constant A is the product including all the primes in the following form
So, the D(S[p+1]) = A
And what’s even more interesting the density of any other Set for any number n can be calculated using a very simple formula based only on the constant A and the unique divisors of number n.
So, for n=2 (or any power of 2) it would be
For n=6 (but also, 12, 18, 24, etc.) it would be
Etc…
In other words, we can say that the average density of Phi of the set of numbers in form of p+n is generally always equal to the Artin’s constant out of which the influence of primes being the divisors of given n has been excluded.
It occurs that the truth of this relation can be proven using Dirichlet's theorem on primes in arithmetic progressions.
Another interesting feature of such sets of numbers being the primes shifted by a certain value of n is that no matter whether we are moving them forward or backward the average density of Phi of such the set is identical.
So, the D(S[p+n]) = D(S[p-n])
It also happens so, that the average density of Phi of any subset of such sets quickly converges to the value characteristic for the entire set.
The average density of all such Sets is obviously equal to the average density of all the natural numbers (1/Zeta(2)), so we can easily derive from it another interesting formula(s) - for example for the value of the function involving all the unique divisors of all natural numbers.
I believe that this feature (certain value of average density of Phi function) of such sets of numbers in form of p+/-n could be used as a base in attempts for proving the twin (and any other size of the gap) primes conjecture.
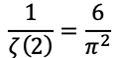






Comments
Post a Comment