PROOF THAT THE RELATIONSHIP BETWEEN MOBIUS AND ZETA FUNCTIONS IS TRUE FOR EVERY S

PROOF THAT THE RELATIONSHIP

IS TRUE FOR EVERY S

Let's start by introducing the concept of Numbers Plane (or Field).

The Numbers Plane is a plane on which each natural number n has its representation in the form of n unities spaced at equal intervals on a circle with radius n.

This is an example representation of the number n=6

And this is how the representation of numbers from n=1 to n=6 looks like.

Additionally, we make a distinction between the unities within each number n as being relatively prime and not relatively prime to n.

To easily distinguish unities, we will mark the relatively prime in red, and not the prime one in blue.

This is an example representation of unities for the number n=6. Unities that are relatively prime to 6 are respectively 1st and 5th.

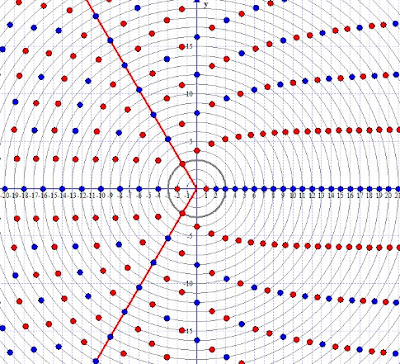
And so, for the numbers from n=1 to n=6

And so, a slice of the entire plane with more n

The sum of the coordinates (resultant) of all the unities within given n always sum up to 0 (x=0, y=0), except for n=1, where obviously the sum is 1 (x=1, y=0)

So, the sum of the coordinates of all unities (belonging to all n from 1 to infinity) on the entire Numbers Plane is equal to 1 (x=1, y=0).

On the other hand, the sum of the coordinates (resultant) of relatively prime unities within a given n is always equal to the value n*µ(n), where µ(n) is a Möbius function.

The above results directly from one of the definitions of the Möbius function.

If from the center of the coordinate system, being the center of the plane, we derive any straight line, then the first unity that is intersected will always be the relatively prime within the given n to which it belongs.

The next ones on this line will be ones that are not relatively prime ones belonging to the numbers 2n, 3n, 4n, etc...

 

If from the center of the coordinate system (center of the plane) we draw rays passing through each of the relatively prime unities belonging to a given n,

Example for n=3

then the sum of coordinates of all the unities (relatively prime coming from the given n and not relatively prime coming from the numbers 2n, 3n, 4n etc…) laying on these rays we can write as

µ(n)*n + µ(n)*2n + µ(n)*3n+…. what is equal to µ(n)*n*(1+2+3+...)

Doing so for every n we are getting the sum of coordinates of all the unities on the Numbers Plane, and the sum is equal to:

µ(1)*1*(1+2+3+…) + µ(2)*2*(1+2+3+…) + µ(3)*3*(1+2+3+…) = 

We know already that the sum of coordinates of all the unities on the plane is equal to 1, so

This is the identity for, let's say, the natural state of the Numbers Plane, in which all unities belonging to the given n lie on a circle with radius n.

 

We can write the above identity as:

Let’s now introduce the general standard notation for the power of "s"

Until now it is assumed that the above is true for s, which Re is > 1

 

In the first step of the proof that s can be any, let's focus on s being a real number (not complex)

 

Let's see how the Numbers Plane and the unities present on it will behave when the power of s changes.

Any change of the power moving in the range from -∞ to +∞  causes the plane to proportional stretching or contracting away from or to the center of the plane, and the unities move along straight lines coming from the center.

But no matter how much the unities are attracted or pulled away from the center, the sum (resultant) of their coordinates will not change and will always be equal to 1.

 

Thus, the said identity is true for every power of s which is a real number.

 

What if the power of s is a complex number?

When the power s is changed, to the movement of the unities along the straight lines towards or from the center of the plane (in the case of real s) will be added also the rotation around the origin of the plane proportional to n and the imaginary part of the complex power.

Unities as the power of s changes will not move along straight lines (as in the case of s being real) but along the arms of logarithmic spirals.

However, since the rotation of the unities within a given n by any angle does not change the sum (resultant) of the coordinates of these unities, regardless of the rotation made, this sum within a given n is always equal to 0 (x=0, y=0), except for n=1, where the unity does not move, so the sum of its coordinates (actually one) is always 1 (x=1, y=0)

 

So regardless of the rotation of all the n, the sum of the coordinates of all the unities on the plane is still equal to 1.

So even using the power of s being any complex number, when changing the power, we observe contraction or stretching of the plane with an additional rotation around the center, but this movement does not change the overall sum (resultant) of the coordinates of all unities on the plane being changed in this way. And this sum is always equal to 1.

So the identity

IS TRUE FOR ANY S